Aufgabe: Tangens, Sinus, Cosinus gleichschenkliges Dreieck 5
Von einem gleichschenkligen Dreieck kennt man c = 40 mm und α = 48,2°.
a) Winkel γ
b) Seitenkante a
c) Flächenhöhe hc
d) Flächenhöhe ha
Lösung:
a) Wir berechnen die Winkel gamma:
γ = 180° – 2 * α
γ = 180° – 2 * 48,2°
γ = 83,6°
b) Seitenkante a
Ankathete (AK) = hc Gegenkathete (GK) = c/2 Hypotenuse (H) = a
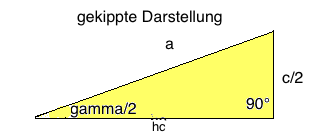
sin γ /2 = GK : H
sin γ /2 = c/2 : a
sin 41,8° = 20 : a / * a
sin 41,8° * a = 20 / : sin 41,8°
a = 20 : sin 41,8°
a = 30,01 mm
A: Die Seitenkante a ist 30,01 mm lang.
c) Wir berechnen die Flächenhöhe hc
hc = √ a² – (c/2)²
hc = √(30,01² – 20²)
hc = 22,37 mm
A: Die Flächenhöhe hc ist 22,37 mm lang.
d) Wir berechnen die Flächenhöhe ha
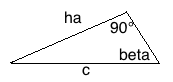
Gegenkathete (GK) = ha Hypotenuse (H) = c
Vorbemerkung: β = α
sin β = GK : H
sin β = ha : c
sin 48,2° = ha : 40 / * 40
ha = sin 48,2° * 40
ha = 29,82 mm
A: Die Flächenhöhe ha ist 29,82 mm lang.
