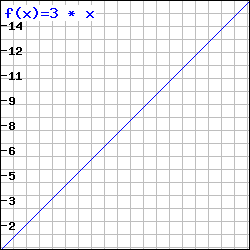Direkte Proportionalität:

Hier erhältst du einen Überblick zum Thema: Direkte Proportionalität | Definition & Eigenschaften
Direkte Proportionalität wird in vielen Bereichen der Mathematik und Naturwissenschaften verwendet, um lineare Beziehungen zwischen Variablen zu beschreiben.
Weitere Lerneinheiten: Übungen | Übungsblätter
I. Definition:
Unter direkter Proportionalität in der Mathematik versteht man eine Beziehung zwischen zwei Größen, bei der die eine Größe mit der anderen im gleichen Verhältnis wächst oder abnimmt.
Das bedeutet, wenn eine Größe verdoppelt wird, verdoppelt sich auch die andere; wenn eine Größe halbiert wird, halbiert sich auch die andere.
II. Berechnung:
Eine proportionale Zuordnung ist ein mathematisches Verfahren, um aus drei gegebenen Werten eines Verhältnisses den unbekannten vierten Wert zu berechnen.
Die direkte Proportionalität kann mit dem Proportionalitätsfaktor berechnet werden:
Der Ausgangswert (x) jeweils multipliziert mit dem Proportionalitätsfaktor (k) ergibt den zugeordneten Wert (y).
Das ergibt folgende Formel:
y = k • x
III. Eigenschaften der direkten Proportionalität
1. Lineare Beziehung:
Bei direkter Proportionalität besteht eine lineare Beziehung zwischen zwei Größen. Das bedeutet, wenn eine Größe zunimmt, nimmt die andere im gleichen Verhältnis zu, und wenn eine Größe abnimmt, nimmt die andere im gleichen Verhältnis ab.
2. Proportionalitätskonstante:
Die beiden Größen sind durch eine feste Zahl, die sogenannte Proportionalitätskonstante (k), miteinander verbunden. Diese Konstante bleibt für alle Werte der Größen gleich.
y = k • x
Hierbei ist y die abhängige Größe, x die unabhängige Größe, und k die Proportionalitätskonstante.
3. Gerade Linie:
Im Koordinatensystem stellt eine direkte Proportionalität eine gerade Linie dar, die durch den Ursprung (0,0) verläuft. Dies zeigt, dass wenn x = 0 ist, dann ist auch y = 0
4. Verhältnis bleibt konstant:
Der Quotient von zugeordnetem Wert y und Ausgangswert x ist konstant. Für alle Paare (x,y) gilt y/x = k
5. Multiplikative Skalierung:
Bei direkter Proportionalität ändert sich eine Größe um den gleichen Faktor wie die andere. Wenn x um einen bestimmten Faktor multipliziert wird, wird y ebenfalls um denselben Faktor multipliziert.
6. Wertepaare:
Die Wertepaare im Koordinatensystem einer direkten Funktion ergeben eine Halbgerade (Strahl).
IV. Beispiel für direkte Proportionalität:
1 kg Äpfel kostet 2 Euro, wie viel kosten 2 (4) Äpfel der gleichen Sorten.
Wir definieren die Variablen:
x = Mengeneinheit: 1, 2 und 4 kg Äpfel.
k = Preis: für je 1 kg Äpfel = 2 Euro
→ hier 2 Euro = Proportionalitätsfaktor
y = k • x
y = Preis bei angegebener Menge
1 ↦ 2 • 1 = 2 Euro
2 ↦ 2 • 2 = 4 Euro
3 ↦ 2 • 4 = 8 Euro
A: 2 kg Äpfel kosten 4 Euro und 4 kg Äpfel kosten 8 Euro.
V. Wichtigste Darstellungsformen:
a) Pfeildiagramme:
1 ↦ 3 • 1 = 3
2 ↦ 3 • 2 = 6
3 ↦ 3 • 3 = 9
4 ↦ 3 • 4 = 12
b) Wertetabellen:
Diese können waagrecht oder senkrecht verwendet werden.
| x | 1 | 2 |
3 | 4 |
| y | 3 | 6 | 9 | 12 |
c) Koordinatensystem:
Mit Punkten im Koordinatensystem kann man einen Halbstrahl zeichnen.
(1/3) (2/6) (3/9) (4/12)