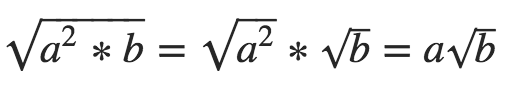Partielles Wurzelziehen 📌 bei Quadratwurzeln

Partielles Wurzelziehen 📌 bei Quadratwurzeln

---

 

Alles, was du wissen musst: Partielles Wurzelziehen 📌 bei Quadratwurzeln

Beim partiellen Wurzelziehen wird nur von den quadratischen Bestandteile die Wurzel gezogen, nachdem wir Teilwurzeln gebildet haben. 

Zusätzliche Lernmaterialien: Aufgaben | Übungen und Partielles W. | Übungsblätter zum Ausdrucken!

Definition: Partielles Wurzelziehen

---

Beim teilweisen Wurzelziehen, auch partielles Radizieren genannt:

1.wird der Ausdruck unter der Wurzel in mehrere Faktoren (Wurzeln) zerlegt

2. und dann wo möglich vereinfacht.

Bei der Zerlegung wird darauf geachtet, dass wir Teilwurzeln bilden, die quadratische Radikanden aufweisen. 

 

Bei einer Quadratwurzel können dann alle Faktoren vereinfacht werden, die quadratisch sind.

Beispiele: √9 = 3, √a² = a, √100 = 10

Die nicht quadratischen Faktoren verbleiben hingegen unter der Wurzel. 

Beispiele: √3, √a, √11

 

Formel:

---

Hier findest du die Formel für das partielle (teilweise) Wurzelziehen.

Sie ist nach dem Distributionsgesetz (Verteilungsgesetz) für die Multiplikation aufgebaut.

 

Und zwar können durch die Aufteilung die quadratischen Wurzelelemente  (z.B. √a²) von den nicht quadratischen Wurzelelementen (√a) getrennt werden. 

a² = quadratisches Element

b = nichtquadratisches Element

 

Beispiel 1: 

---

Vereinfache √200

1. Schritt: zerlegen

Wir zerlegen √200 so,  dass eine Teilwurzel einen quadratischen Radikanden (hier rot)  aufweist.

√200  = √100  • √2  

 

2. Schritt: Wo möglich die Wurzeln ziehen

quadratische Radikanden: aus √100  wird 10 

nicht quadratische Radikanden: √2  bleibt

d.f. 10 • √2  

Beispiel 2:

---

Vereinfache √75x²y³

1. Schritt zerlegen:

Wir zerlegen √75x²y³  so,  dass möglichst viele Teilwurzeln quadratischen Radikanden (hier rot) aufweisen.

√75x²y³ = √25  • √3  • √x²  • √y²  •√y

 

2. Schritt: Wo möglich die Wurzeln ziehen

quadratische Radikanden:

aus √25  wird 5      

aus √x²  wird x        

aus √y²  wird y

 

nicht quadratische Radikanden:

√3  bleibt       

√y bleibt

d.f. 5xy • √3y 

 

• Partielles Wurzelziehen Merkblatt 
• Partielles Radizieren Übungsblatt
• Partielles Radizieren Aufgabenblatt 1