Definition: lineare Funktion
Das Element der Definitionsmenge x, wird als Argument oder unabhängige Variable bezeichnet.
Das zugeordnete Element der Zielmenge y, wird als Funktionswert bzw. abhängige Variable bezeichnet.
Zuordnungsvorschrift:
Die Zuordnungsvorschrift ist oft ein Term.
Wie viel kosten x kg?
→ Zuordnungsvorschrift: y = 3x
Die Funktion kann angegeben werden durch eine Wertetabelle, einen Funktionsterm oder durch einen Graphen.
Normalform einer linearen Funktion:
Der Graph einer linearen Funktion ist eine Gerade mit der Steigung k, die die y-Achse im Punkt (0/d) schneidet.
Termdarstellung:
y = k • x + d oder f (x) = k • x + d
k = Steigung der Geraden
d = Schnittpunkt mit der y-Achse ⇒ Punkt (0/d)
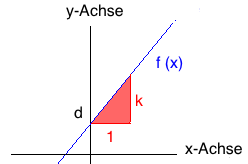
Ermittlung der Steigung k der Geraden:
Die Steigung der Geraden durch die Punkte R (x1/y1) und S (x2/y2) ist definiert durch
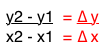
Beispiele für Steigungen:
Vorbemerkung:
positive k-Werte (k > 0) = steigende Gerade
negative k-Werte (k < 0) = fallende Gerade
flach steigend: z.B. k = 0,5
flach fallend: z.B. k = – 0,5
steil steigend: z.B. k = 4
steil fallend: z.B. k = – 4
Arten von linearen Funktionen:
a) Inhomogene Funktion z.B. y = 2x + 3 (d ≠ 0 und k ≠ 0)
b) Homogene Funktion z.B. y = 2x (d = 0)
c) Konstante Funktion z.B. y = 3 (k = 0)
Weitere wichtige Begriffe:
Nullstelle: Punkt an der f (x) = 0
graphisch: der Schnittpunkt der Geraden mit der x-Achse
Fixwert: Punkt an der f (x) = x
graphisch: Schnittpunkt des Graphen mit der 1. Mediane (Gerade, die durch den Ursprung verläuft und eine Steigung von 45° aufweist).
Beispiel:
Bestimme von folgender Funktion y = 2x – 3 die Steigung k und d.
Stelle zudem die Funktion graphisch dar.
1. Schritt: Wir ermitteln k und d
y = 2x – 3
Wir können die Werte für k und d direkt aus der Geradengleichung ablesen!
Steigung: k = 2 (steigende Gerade)
Schnittpunkt mit der y-Achse: d = – 3
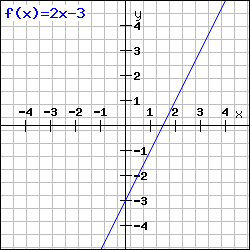
2. Schritt: Wir stellen die Funktion graphisch dar
Ermittlung von 2 Punkten:
Wir setzen den x-Wert in die Funktion f(x) = 2x – 3 ein!
f (0) = 2 (2 • 0 – 3 = – 3) ⇒ P1 (0/-3)
f (1) = 1 (2 • 1 – 3 = – 1) ⇒ P2 (1/-1)
Tests:
Funktion allgemeine Definition Test
Lineare Funktion Steigung, Nullstelle
Lineare Funktion Steigung k Test
Lineare Funktion Überblick Test
PDF-Übungsblätter:
Lineare Funktion Überblick Merkblatt
Lineare Funktion Steigung k Übungsblatt

