Aufgabe: Volumensrotation y-Achse Übung 1
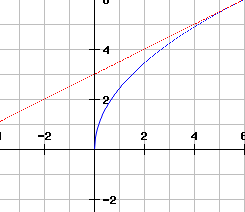
Gegeben ist die Funktion f: y² = 6x.
Die Tangente im Punkt P (6/y >0), der Graph der Funktion und die y-Achse begrenzen ein Flächenstück.
Berechne das Volumen des Drehkörpers, wenn das Flächenstück um die y-Achse rotiert.
Lösung: Volumensrotation y-Achse Übung 1
1. Schritt: Wir berechnen den Punkt der Funktion
y² = 6x / √
⇒ y = √6x
Wir geben für x den Wert 6 in die Funktion ein ⇒ y = √(6*6)
f (6) = +/- 6 ⇒ P (6/6)
2. Schritt: Wir berechnen die Tangente
y² = 6x ⇒ y = √6x
Wir bilden die 1. Ableitung:
y´ = 0,5 * (6x)-0,5 * 6
y´= 3/√6x
Wir ermitteln die Steigung k der Tangente:
y´= 3/√(6*6)
y´(6) = 1/2 d.f. k = 0,5
Wir ermitteln d der Tangente:
y = kx + d
6 = 0,5*6 + d
d.f. d = 3
Tangente t: y = 0,5x + 3
3. Schritt: Wir berechnen den Schnittpunkt
Wir setzen die gegebene Funktion der Tangente gleich
√6x = 0,5x + 3 /²
6x = 0,25x² + 3x + 9 / – 6x
0 = 0,25x² – 3x + 9 /: 0,25
x² – 12x + 36 = 0 ⇒ (x – 6)² ⇒ x = 6
d.f. f (6) = 6 S (6/6)
4. Schritt: Wir berechnen das Volumen der f
Anmerkung: Da Rotation um y-Achse – formen wir um auf x²
y² = 6x / : 6
x = y²/6 /²
x² = y4/36
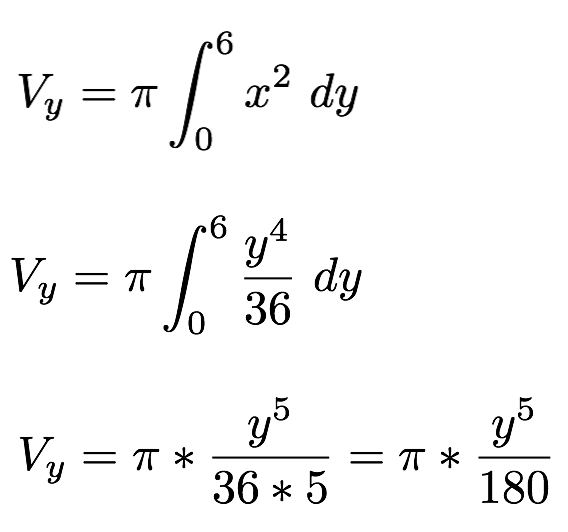
V = π * 65/180 – 0
V = 43,2π
5. Schritt: Wir berechnen das Volumen des Kegels
Anmerkung: Die Tangente in Rotation um die y-Achse bildet einen Hohlkegel.
V = r² * π * h : 3
V = 36 * π * 3 : 3
V = 36π
6. Schritt: Wir berechnen das Gesamtvolumen
V = Vf – VK
V = 43,2π – 36π
V = 7,2π VE
A: Das Volumen des Drehkörpers beträgt 7,2*π VE.
