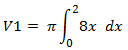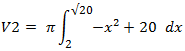Aufgabe: Volumensrotation x-Achse Übung 1
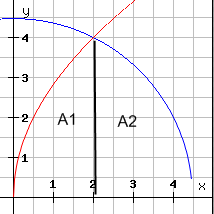
Durch den Punkt P (2/4) gehen ein Kreis k in Mittelpunktslage und eine Parabel in erster Hauptlage.
Das gemeinsame Flächenstück der beiden Kurven rotiert um die x-Achse.
Berechne das Volumen des dabei entstehenden Körpers!
Lösung: Volumensrotation x-Achse Übung 1
1. Schritt: Wir stellen eine Kreisgleichung auf
Wir ermitteln den Kreisradius:
r = √ (2² + 4²) ⇒ r = √20
Kreisgleichung:
k: x² + y² = 20 / – x²
d.f. y² = – x² + 20
2. Schritt: Wir stellen eine Parabel in der 1. Hauptlage auf:
p: y² = 2px
16 = 2*p*2 / : 4
p = 4
d.f. y² = 8x
3. Schritt: Wir berechnen den Schnittpunkt
Wir setzen die Kreisgleichung der Parabel gleich
– x² + 20 = 8x /+ x² – 20
x² + 8x – 20 / Vieta
x1,2 = – 4 +/- √ (4² + 20)
x1,2 = – 4 +/- 6
d.f. (x1 = – 10) und x2 = 2
d.f. P = (2/4)
4. Schritt: Wir berechnen das Volumen
Parabel: y = √(8x) Kreisgleichung: y = √(- x² + 20)
Volumen der Parabel
Formel:
Wir integrieren:
V1 = π * 8x²/2 ⇒ V1 = π * 4x² [2; 0]
V1 = π * (4 * 2² – 0)
V1 = 16π VE
Volumen der Kreisgleichung
Formel:
Die obere Grenze des bestimmten Intervall ist der Radius des Kreises (√20), die untere Grenze ist der Schnittpunkt mit der Parabel (2).
V2 = π * (- x³/3 + 20x) [√20; 2]
V2 = π * [(-(√20)³/3 + 20 * √20) – (-(2)³/3 + 20 * 2)]
V2 = π * [59,628… – 37,33…]
V2 = 22,30π VE
V = V1 + V2
V = 16π + 22,3π
V = 38,3π VE
A: Das Volumen des Drehkörpers beträgt 38,3π VE.