Vektoren Lagebeziehung von Geraden:
Im Folgenden werden die Lagebeziehungen von Geraden hinsichtlich der Berechnung mit Vektoren besprochen.

Gegenseitige Lage von Geraden in der Ebene:
Zwei Geraden in der Ebene: können folgende gegenseitige Lage einnehmen:
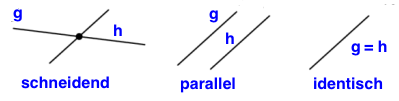
a) g und h schneiden einander in einem Punkt (Schnittpunkt):
g ∩ h = {S}
b) g und h sind parallel und verschieden:
g ∩ h = {}
c) g und h sind parallel und zusammenfallend (identisch):
g ∩ h = {g = h}
Berechnung:
1. Fallunterscheidung: parallel oder nicht parallel
mit Hilfe des Parallelitätskriterium bestimmen wir, ob die beiden Geraden parallel sind oder nicht.
Sind sie nicht parallel → schneiden sie sich (liegt ein Schnittpunkt vor)
2. Fallunterscheidung: parallel oder identisch
Ergibt die 1. Fallunterscheidung eine Parallelität, erfolgt im 2. Schritt die Unterscheidung ob parallel und verschieden oder parallel und zusammenfallend.
Sind die beiden Geraden identisch, muss der Punkt X1 der 1. Geraden, auch auf der 2. Geraden liegen.
Oder der Punkt X2 der 2. Geraden, muss auch auf der 1. Geraden liegen.
Beispiel:
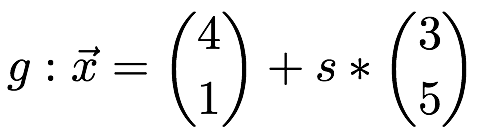
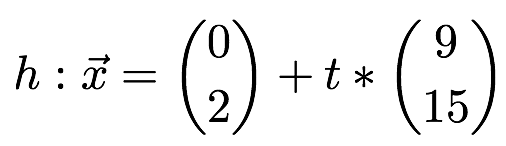
1. Fallunterscheidung: parallel oder nicht parallel:
Dazu setzen wir jeweils die beiden Richtungsvektoren gleich
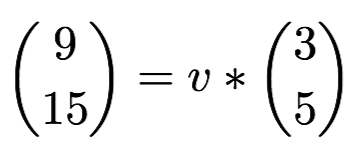
Aufspaltung in x und y Komponente:
3 = v • 9 / : 9
d.f. v = + 1/3
5 = v • 15 / : 15
d.f. v = + 1/3
1/3 ist gleich 1/3 w.A.
d.f. Die beiden Vektoren sind parallel.
2. Fallunterscheidung parallel verschieden oder identisch:
Um dies zu überprüfen setzen wir den Punkt X2 der 2. Geraden in die 1. Gerade ein:
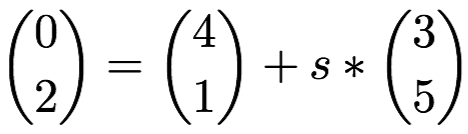
Aufspaltung in x und y Komponente:
0 = 4 + s • 3 / – 4
d.f. – 4 = 3 • s / : 3
d.f. s = – 4/3
2 = 1 + s • 5 / – 1
d.f. 1 = 5 • s / : 5
d.f. s = 1/5
– 4/3 ist gleich 1/5 f.A.
d.f. Die beiden Vektoren sind parallel verschieden (und nicht identisch)
