Definition: Scheitelpunktform
Mit der Scheitelpunktform einer quadratischen Gleichung kann der Scheitelpunkt direkt abgelesen werden.

Definition: Scheitelpunkt
Unter dem Scheitelpunkt versteht man den tiefsten bzw. den höchsten Punkt einer quadratischen Funktion (Parabel).
Ist die Parabel nach oben geöffnet , so ist Scheitelpunkt der tiefste Punkt der Funktion (Minimum).
Ist die Parabel nach unten geöffnet, so ist Scheitelpunkt der höchste Punkt der Funktion (Maximum).
Formel der Scheitelpunktform einer quadratischen Funktion:
Daraus lassen sich die Koordinaten des Scheitelpunkts direkt ablesen S (d | e).
Beispiel:
Bestimme aus folgender Funktion den Scheitelpunkt:
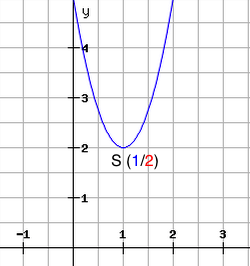
f(x) = 3 * (x – 1)² + 2
→ Scheitelpunkt: S (1|2) → Minimum
Allgemeine Form in Scheitelpunktform umrechnen:
Ist die quadratische Funktion in der Form von ax² + bx + c gegeben, so wird der Scheitelpunktform mit Hilfe der quadratischen Ergänzungsmethode berechnet.
Beispiel:
allgemeine quadratische Form: f (x) = x² + 2x + 3
gesucht: Scheitelpunktform und Scheitelpunkt?
Lösung:
Methode des quadratischen Ergänzens:
x² + 2x + 3 / – 3
x² + 2x + ? = – 3
x² + 2x + 1² = – 3 + 1²
(x + 1)² = – 2 / + 2
d.f. f (x) = (x + 1)² + 2
d.f. S (- 1/2)
