Quadratische Funktion:
Funktionen der Art f (x) = ax² + bx + c für die gilt: a, b, c ∈ ℝ mit a ≠ 0 sind quadratische Funktionen.
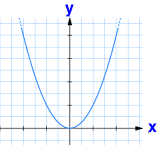
Der dabei entstehende Graph ist eine Parabel:
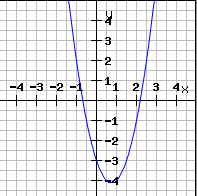
Parameter a, b, c:
Durch die Veränderung des Parameters a kann die Funktion gestreckt, gestaucht oder an der x-Achse gespiegelt werden.
Es gelten folgende Zusammenhänge:
a > 0 → Die Parabel ist nach oben geöffnet.
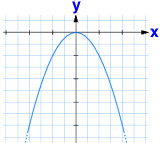
a < 0 → Die Parabel ist nach unten geöffnet.
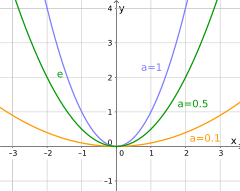
|a| < 1 → Die Parabel ist in Richtung der y-Achse gestaucht (erscheint breiter).
Abb. Wikipedia
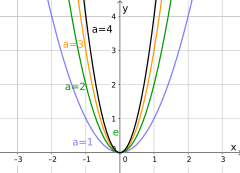
|a| > 1 → Die Parabel ist in Richtung y-Achse gestreckt (erscheint schmaler und steiler).
Abb. Wikipedia
– a (Vorzeichenwechsel) → Spiegelung der Parabel an der x-Achse.
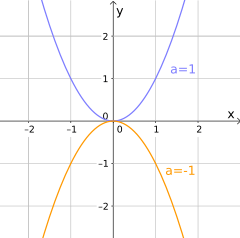 Abb. Wikipedia
Abb. WikipediaDer Parameter b bestimmt die Steigung der Parabel im Schnittpunkt der y-Achse.
b + 1 → dann wird der Graph um 1/2a nach links und um (2b + 1) / 4a nach unten verschoben.
b – 1 → dann wird der Graph um 1/2a nach rechts und um (2b + 1)/ 4a nach oben verschoben.
Wird der Parameter c verändert, so bewirkt dies eine Verschiebung in die y-Richtung:
c + 1 → dann wird der Graph um eine Einheit nach oben verschoben
c – 1 → dann wird der Graph um eine Einheit nach unten verschoben
Diskriminante:
Vorbemerkung:
Die Diskriminante (b² – 4ac) oder (p/2)² – q entscheidet über die Anzahl der Lösungen der quadratischen Gleichung
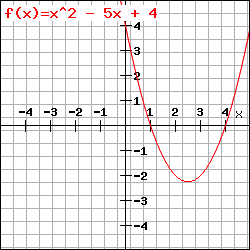
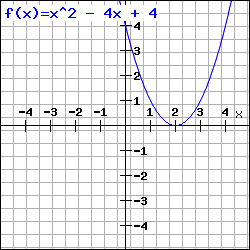
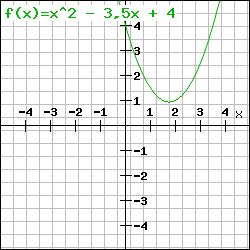
Berechnung der Nullstellen:
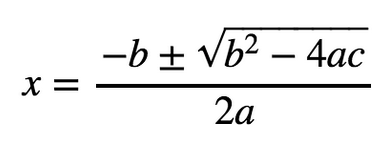
Minimum/Maximum (Scheitelpunkt):
Definition:
Der Scheitelpunkt ist entweder:
– der tiefste Punkt (absolute Minimum) einer Parabel, die nach oben geöffnet ist.
– der höchste Punkt (absolute Maximum) einer Parabel, die nach unten geöffnet ist.
Bei a < 0 liegt ein Maximum vor.
Die Parabel öffnet sich nach unten.
Bei a > 0 liegt ein Minimum vor.
Die Parabel öffnet sich nach oben.
a) Berechnung mit der Scheitelpunktformel:
Liegt die Funktion in der Scheitelpunktform vor, können die Koordinaten des Scheitelpunktes direkt abgelesen werden.
f (x) = a • (x – xs)² + ys → S (xs/ys)
Tests:
Quadratische Funktion Scheitelpunkt
Übungsblätter:
Parabel Diskriminante Übungsblatt
Parabel Parameter a verändern Übungsblatt
Parabel Parameter a, b, c Übungsblatt
Merkblätter:
Parabel Diskriminante Merkblatt