Parallele lineare Funktion Termdarstellung:
Wir ermitteln die Termdarstellung einer parallelen Gerade:
1. indem wir die Steigung der ursprünglichen Geraden (k) übernehmen (kp)
2. und mit der übernommenen Steigung kp und einem Punkt der neuen Geraden d berechnen
3. Jetzt können wir eine Termdarstellung der parallelen Geraden bilden.
Beispiel:
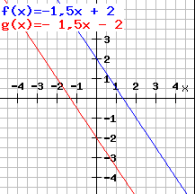
Ermittle zur Geraden f: y = – 1,5x + 2 die parallele Gerade g, die durch den Punkt (-1/-0,5) geht.
1. Schritt: Wir ermitteln die neue Steigung. k = kp
k = – 1,5 ⇒ parallele Gerade: kp = – 1,5
2. Schritt: Wir ermitteln d der parallelen Geraden g:
kp = – 1,5 und Punkt (-1/-0,5) d.f. x = -1 und y = -0,5
g: y = kpx + d
– 0,5 = – 1,5 • (- 1) + d
– 0,5 = + 1,5 + d / – 1,5
– 2 = d
3. Schritt: Wir ermitteln die Termfunktion der parallelen Geraden.
d.f. g: f (x) = – 1,5x – 2
Graphische Darstellung:
PDF-Übungsblätter:
Parallele lineare Funktion Termdarstellung Merkblatt
Parallele lineare Funktion Termdarstellung Übungsblatt