Inverse lineare Funktion aufstellen:
Eine Bildung einer Umkehrfunktion (inversen Funktion) ist dann möglich, wenn nicht nur zu jedem Argument (x) eindeutig ein Funktionswert (y) zugeordnet ist, sondern wenn auch umgekehrt zu jedem Funktionswert (y) genau ein Argument (x) gehört.
Diese Voraussetzung ist bei linearen Funktionen erfüllt.

Beispiel einer Umkehrfunktion:
1 kg Bananen kosten 3 € d.f. Funktion: f: y = 3x
Um 3 € erhalte ich 1 kg Bananen
d.f. Umkehrfunktion: f-1: x → y = x/3
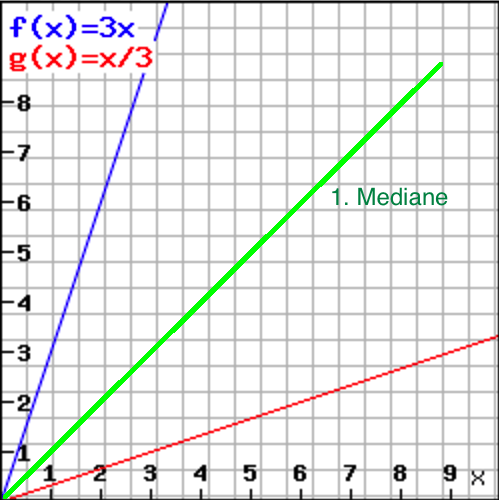
Graphen der Umkehrfunktion:
Den Graphen der Umkehrfunktion f-1: 3x → g (x) = x/3 erhält man, wenn man den Graphen von f an der 1. Mediane spiegelt.
Die 1. Mediane ist eine Gerade, die durch den Ursprung verläuft und eine Steigung von 45° aufweist.
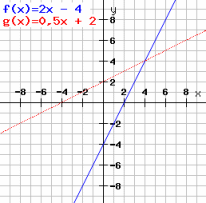
Termdarstellung einer inversen linearen Funktion:
Wir ermitteln die Termdarstellung einer inversen linearen Funktion.
1. indem wir die Variablen x und y vertauschen
2. und mit Hilfe von Äquivalenzumformungen y isolieren.
Beispiel für eine Umkehrfunktion:
gegeben: y = 2x – 4
gesucht: Umkehrfunktion
1. Schritt: Wir vertauschen x und y
x = 2y – 4
2. Schritt: Wir formen auf y um
x = 2y – 4 / + 4
x + 4 = 2y / : 2
y = 0,5x + 2
d.f. Umkehrfunktion f-1: x → y = 0,5x + 2
3. Schritt: Graphische Darstellung: