Indirekte Proportionalitätsfunktionen:
Ist f eine reelle Funktion mit f (x) = f (x) = k : x (mit k ≠ 0 und x ≠ 0), so nennt man diese eine indirekte Proportionalitätsfunktion oder Reziprokfunktion.
Die Funktionswerte f (x) sind zu den Argumenten x indirekt proportional.
Es besteht kein linearer Zusammenhang zwischen den Funktionswerte f (x) zu den Argumenten.
Graphische Darstellung:
P (x) = 4 : x Der Graph ist symmetrisch bezüglich des Ursprungs.
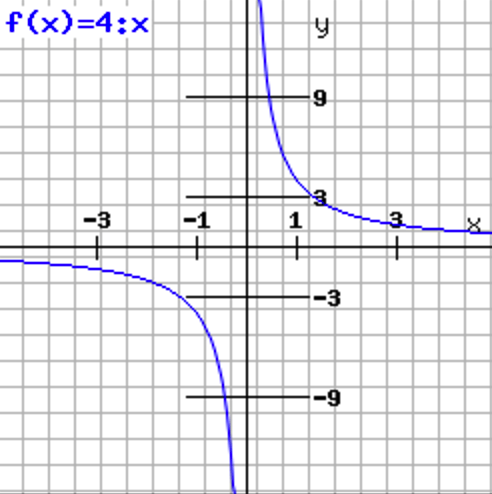
Eigenschaften:
a) f (a * x) = f (x) : a → Dem a-fachen Argument entspricht der a-te Teil des Funktionswertes.
b) k = f (1) → Die Konstante k ist der Funktionswert an der Stelle 1.
c) f (x) * x = k → Das Produkt aus Funktionswert und Argument ist hier konstant.
Beispiel:
Die Funktionswerte f (x) einer Funktion f seien zu den Argumenten indirekt proportional:
f (10) = 0,5 Gib eine Termdarstellung an!
Lösung:
k = f (x) * x
k = 10 * 0,5
k = 5
d.f. f (x) = 5
x
