Pythagoras Parallelogramm alpha kleiner 90 Grad

Pythagoras Parallelogramm alpha kleiner 90 Grad

---

Hier findest du die Lerneinheit: Pythagoras Parallelogramm alpha kleiner 90 Grad

Beim Parallelogramm erhalten wir die benötigten rechtwinkligen Dreiecke  mit der Hilfsgröße m. 

Weiteres Übungsmaterial: Aufgaben | Übungen | Übungsblätter | Merkblatt | Pythagoras 

 

Beim Parallelogramm gibt zwei Möglichkeiten. α < 90° oder α > 90°.

Alle folgenden Berechnungen beziehen sich auf den Sachverhalt α < 90°

Skizze Parallelogramm α < 90°

---

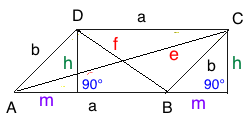
Hilfsgröße m:

---

  →  m = √(b² – h_a²)

 

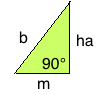
Um aus dem Parallelogramm rechtwinklige Dreiecke zu erhalten, müssen wir zuerst die Hilfsgröße “m” ermitteln.

 

Die Hilfsgröße “m” wird ermittelt, indem wir vom Parallelogramm ein Teildreieck, welches mit der Höhe “ha” und der Seite b gebildet wird abspalten: m² = b² – ha²

 

Rechtwinkliges Dreieck Diagonale “e”:

---

 

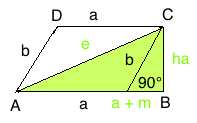
Satz des Pythagoras Diagonale “e”:

Grundformel: e² = (a + m)² + h_a²

Praktische Anwendung:

e = √(a + m)² + h_a²

h_a = √e² – (a + m)²

a + m = √e² – h_a²

 

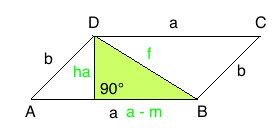
Satz des Pythagoras Diagonale “f”:

---

Praktische Anwendung:

f = √(a – m)² + h_a²

h_a = √f² – (a – m)²

a – m = √f² – h_a²       

 

Beispiel:

Lösung:

1. Schritt: Hilfsgröße m

m = √b² – ha²

m = √(30² – 25,5²)

m = 15,8 cm

2. Schritt: Diagonale e:

e = √ha² + (a + m)²

e = √(25,5² + 63,8²)

e = 68,7 cm

A: Die Diagonale e beträgt 68,7 cm.