Aufgabe: Pythagoras rechtwinkliges Dreieck Musterbeispiel 1
Rechtwinkliges Dreieck a = 4,5 m b = 6,2 m
a) Hypotenuse c = ? b) Flächeninhalt = ?
Lösung: Pythagoras rechtwinkliges Dreieck Musterbeispiel 1
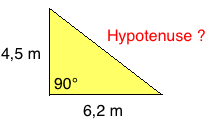
Überlegung:
Die gesuchte Seite c liegt gegenüber dem rechten Winkel – daher plus unter der Wurzel!
a) Berechnung von c:
c = √ a² + b²
c = √ (4,5² + 6,2²)
c = 7,77 m
A: Die Hypotenuse c ist 7,77 m lang.
b) Berechnung vom Flächeninhalt:
A = a • b : 2
A = 4,5 • 6,2 : 2
A = 13,95 m²
A: Der Flächeninhalt beträgt 13,95 m².
