Definition: größter gemeinsamer Teiler (ggT)
Der ggT ist der größte gemeinsame Teiler einer Teilermenge von zwei oder mehreren natürlichen Zahlen.
Anders formuliert ist das ggT das Produkt der gemeinsamen Teiler der vorgegebenen Zahlen.
Hinsichtlich der Lösungsbildung gibt es zwei Verfahren:
a) für kleinere Zahlen genügt die einfache Bildung der Teilermengen
b) bei größeren Zahlen ist die Primfaktorenzerlegung vorteilhaft.
Bildung mittels Teilermengen:
Anwendungsgebiet:
bei kleineren Zahlen
Vorgangsweise:
1. Wir bilden von jeder Zahl die Teilermenge.
2. Wir bestimmen durch Vergleich den größten gemeinsamen Teiler
Beispiel:
Bilde den ggT (16, 20)
1. Schritt: Wir bilden die Teilermengen:
T (16) = {1, 2, 4, 8, 16}
T (20) = {1, 2, 4, 5, 10, 20}
2. Schritt: Wir bestimmen den größten gemeinsamen Teiler
d.f. ggT (16, 20) = 4
Bildung mit Primfaktorenzerlegung:
Anwendungsgebiet:
bei größeren Zahlen
Vorgangsweise:
1. Wir bilden von jeder Zahl die Primfaktorenzerlegung.
2. Wir suchen die Teiler, die in allen Zahlen gemeinsam vorkommen.
3. Wir bilden das Produkt der gemeinsamen Teiler und erhalten dadurch den ggT.
Beispiel:
Bilde den ggT (28, 40)
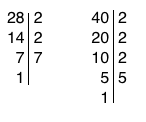
Zerlege 28 in Primfaktoren: 28 = 2 • 2 • 7
Zerlege 40 in Primfaktoren: 40 = 2 • 2 • 2 • 5
2. Schritt: Wir suchen die gemeinsamen Teiler
28 = 2 • 2 • 7
40 = 2 • 2 • 2 • 5
3. Schritt: Wir bilden mit dem Produkt der gemeinsamen Teiler den ggT
ggT (28, 40) = 2 • 2 = 4
Relativ prim:
Eine Ausnahme bei der Bildung des ggT sind die teilerfremden Zahlen, die auch relativ prim genannt werden.
Da sie keine gemeinsamen Teiler aufweisen, ist ihr größter gemeinsamer Teiler immer 1.
Davon sind vor allem auch Primzahlen betroffen.
1. Schritt: Wir bilden die Teilermengen:
T(17) = {1, 17}
T(18) = {1, 2, 3, 6, 9, 18}
2. Schritt: Wir bestimmen den größten gemeinsamen Teiler
T(17) = {1, 17}
T(18) = {1, 2, 3, 6, 9, 18}
Tests:
größte gemeinsame Teiler (ggT)
Videos:
PDF-Übungsblätter:
ggT mit Primfaktorenzerlegung bilden Übungsblatt
ggT mittels Teilermengen ermitteln Übungsblatt 1
größte gemeinsame Teiler (ggT) Übungsblatt 1
ggT Lernzielkontrolle Übungsblatt
ggT und kgV mit Primfaktorenzerlegung Übungsblatt 1

