Definition eines Bruches:
Ein Bruch ist eine nicht ausgeführte Division.
z.B. 3/4 = 3 : 4
Dies ist vor allem beim Anschreiben von Periodenzahlen ein großer Vorteil!
z.B. 1/3 (statt 0,333….)
Bestandteile eines Bruches:

a) Zähler:
gibt die Anzahl der Bruchanteile an → hier 3
b) Bruchstrich:
gibt einerseits das Verhältnis zwischen Zähler und Nenner an – hier 3 :4
und steht andererseits für eine Rechenoperation (dividieren)
c) Nenner:
gibt an, in wie viele Teile das Ganze unterteilt ist → hier 4
Brucharten:
Nachfolgend sind die wichtigsten Brucharten aufgeführt:
Gemischte Brüche in unechte Brüche umwandeln:
Gemischte Brüche werden in unechte Brüche umgewandelt, indem wir den Zähler neu berechnen und der Nenner wird unverändert gelassen.
Berechnung des neuen Zählers:
Wir multiplizieren die ganze Zahl mit dem Nenner und addieren den Zähler.
Berechnung des neuen Nenners:
Der Nenner wird nicht verändert.
Der neue Zähler wird ermittelt mit 5 • 4 + 3 = 23
Der Nenner bleibt unverändert.
Unechte Brüche in gemischte Brüche umwandeln
Unechte Brüche werden in gemischte Brüche umgewandelt, indem wir den Zähler neu berechnen und der Nenner wird unverändert gelassen.
Das Ergebnis der Division ohne Komma (Quotient) ist ganze Zahl.
Der Rest der Division ist der neue Zähler.
Der Nenner bleibt unverändert.
Wenn nötig, wird der neu entstandene Bruch auch noch gekürzt.
Beispiel:
Wandle 14/3 in einen gemischten Bruch um:
Lösung:
14/3 = 4 2/3
Berechnung: 14 : 3 = 4
2 Rest
ganze Zahl = 4
neuer Zähler = 2
Nenner = 3
Kürzen von Brüchen:
Beim Kürzen von Brüchen werden Zähler und Nenner mit der gleichen Zahl dividiert.
Der Wert eines Bruches bleibt dabei gleich.
Das Kürzen von Brüchen dient allgemein dazu Endergebnisse zu vereinfachen.
Beispiel:
Vorgangsweise:
1. Wir suchen den größten gemeinsamer Teiler → hier 5
2. Wir dividieren Zähler und Nenner durch
Erweitern von Brüchen:
Beim Erweitern von Brüchen werden Zähler und Nenner mit der gleichen Zahl multipliziert.
Der Wert eines Bruches bleibt dabei gleich.
Das Erweitern stellt oft eine Voraussetzung für das Addieren und Subtrahieren von Brüchen dar!
Beispiel:
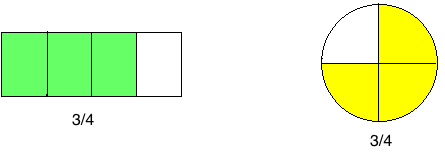
Beispiele für die Darstellung von Brüchen – hier 3/4:
Die farbigen Flächen stellen jeweils den Zähler dar.
hier: grün und gelb – jeweils 3
Die gesamte Anzahl der Flächen stellen den Nenner dar.
hier: grün und weiß bzw. gelb und weiß – jeweils 4